最近在做个小渲染Demo,展示效果需要一些基本图元。基本图元的三角网格均可以程序化生成,这篇文章主要收集了这些生成方法。
前言
图形学中,模型表示的方法很多,它们大致可以分为两类:显式表示(Explicit)与隐式表示(Implicit)。
显式表示的常见方法有:点/线/多边形表示和曲线/曲面表示等。而隐式表示,就可以直接给出几何体表面的定义方程,却不用管其如何求解:
比如对于三维球体,我们知道它的隐式表示为:
实时渲染中我们主要使用的是多边形表示,就需要将几何体的隐式表示转换为显式表示。常用的方法是将隐式表示的方程先转化为参数方程:
参数方程本身作为一种显式表示,其给出了几何体表面的点坐标,再将这些点坐标连接起来形成为多边形网格(一般是三角形)后,就得到了几何体最终的显式表示。
本文主要介绍几种球体的转换方法。
球坐标转换
对于球面来说,最常见的参数化方式是采用球坐标公式。
![球坐标系,图来自[2]](/images/gl_sphere01.png)
图中球坐标系有三个参数:半径, 方位角和倾斜角。如果将球体看做是地球的话,角就是经度,角就是维度。为了方便起见,我们在本文中采用的球坐标系与上图有一些不同(因为实在找不到图了= =):我们将角定义为与z轴的夹角(注意这里z朝上)而不是与xy平面的夹角,这时角表示的是余纬(colatitude),也就是$90^{\circ} - $ 纬度。这样定义的好处是角的取值不会涉及到负数,方便我们进一步处理。
上述定义下的球坐标公式为:
其中两个角的在弧度制下取值范围是和。
接下来的问题是如何给和取值。我们首先想到的自然是均匀取值,也就是用以下的公式:
此处我们把横向(经度)上的划分称为sectors,纵向(维度)上的划分称为stacks。通过控制不同的横向与纵向的分段数,我们就可以控制球体的精度。由于角的范围是角的两倍,为了让生成的球在横向与纵向上有相同密度的点,一般设定,这样控制精度的参数就仅需一个。
球坐标本身经过三角函数的变换,角度上的均匀分布在球面上并不均匀。从下图我们可以看出在南北极的点分布要比赤道上的密一些(如果看成是地球的话)。
![球坐标下分区是不均匀的,图来自[2]](/images/gl_sphere02.png)
点的分布不均导致了每个小区的面积并不相等,不过与生成球面上的随机点不同,这并不妨碍渲染的结果,因为从模型本身的轮廓来说,正视图与俯视图看到的圆都分别有条边和条边,而我们已经设定了它们相等。
有了顶点坐标的计算公式后,下一步就是将顶点连接形成多边形网格。一般我们采用的是三角形网格(Triangle Mesh),需要把上图的四边形切分为2个三角形。由于渲染API一般要利用“背面剔除”特性加速渲染,我们需要保证三角面的顶点顺序一致。如果正面的顶点顺序为逆时针,则一个四边形的两个三角形的顶点就是。储存顶点时,一般可以共享相邻三角形的顶点,以减少储存空间的开销;不过,如果共享顶点的法线、贴图坐标不同的话,就不能采用共享顶点了。
![三角网格,图来自[2]](/images/gl_sphere03.png)
基础模型的一个好处就是具有良好定义的贴图映射、法线信息。对于球来说,其每个顶点的法线就是单位化后的坐标,即。对于球的贴图映射有多种方案,在本方案中可以直接用归一化的方位角和倾斜角来获取,即
由于球坐标的方案与球体UV坐标有很强的关系,这种生成的球体有时也被称作UV球体(UV Sphere)。
以上,球坐标方案的生成代码如下:
1 | const float r = 1.0f; |
上述代码需要注意的是,在顶部与底部的小区块,由于有一个顶点重合,只用绘制一个三角形即可。
细分多面体
细分多面体也是一种常见的创建球体Mesh的方法。其相对UV球体,点的分布更加均匀(UV球体的很多顶点浪费在了靠近南北极的地方),因此用较少的顶点就可以实现不错的精度。
细分的方法也比较简单,对于每个三角形来说,每经过一步,就分裂为4个新的三角形,递归地进行这个过程,就可以得到面数更多更精细的模型。

当然,需要将这些多出来的顶点移到球壳上,不然怎么细分都还是球面。。因为我们已经假定了球心的位置在坐标原点,而球壳上的点到球心的距离为一常数,我们只需要让点沿着过原点的线移动并设定其到原点长度为半径即可。形象的说,这个过程类似把把多边形表面“膨胀”出去的过程,如下图所示:
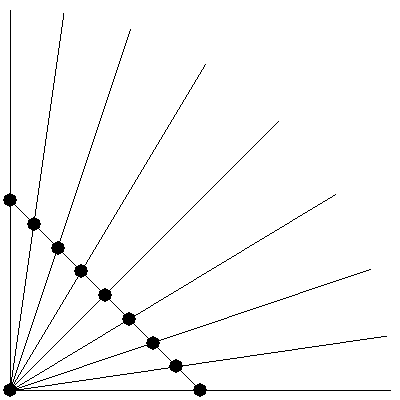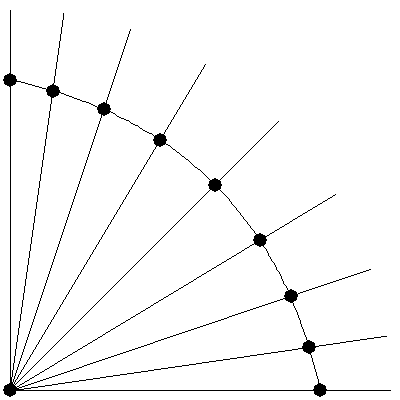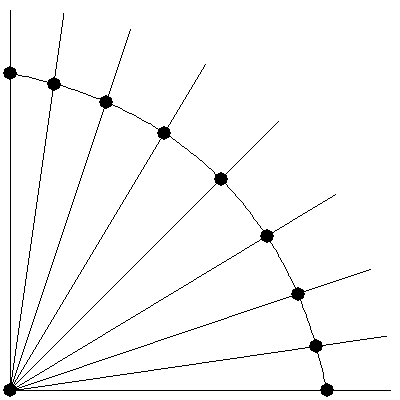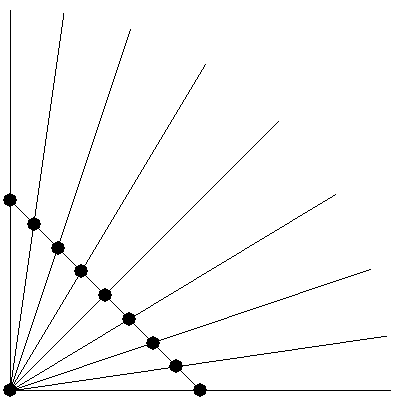
有个这个过程,我们就可以把任意多面体细分为球体了。
下面以正二十面体为例,详细说一下这个过程。
细分正二十面体(Icosphere)
正二十面体本身顶点比较均匀,适合作为基础几何体,这样细分为球体后分布依然会比较均匀。正二十面体有12个顶点,将两个顶点放在顶部与底部,剩下的10个顶点分别在高度为的平面上,且每个平面上的点正好是正五边形。
| 侧视图 | 俯视图 |
|---|---|
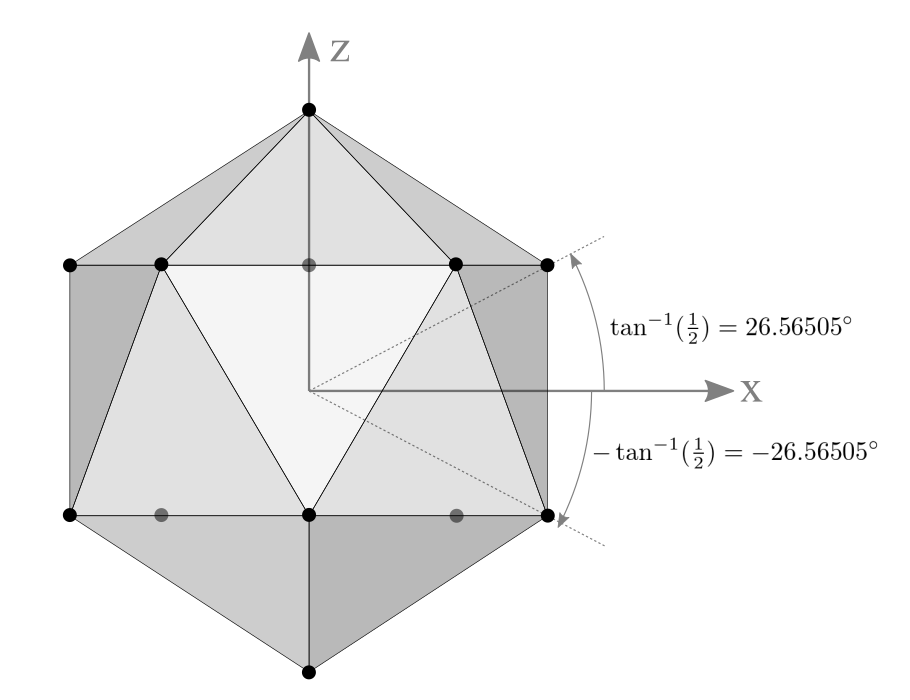 |
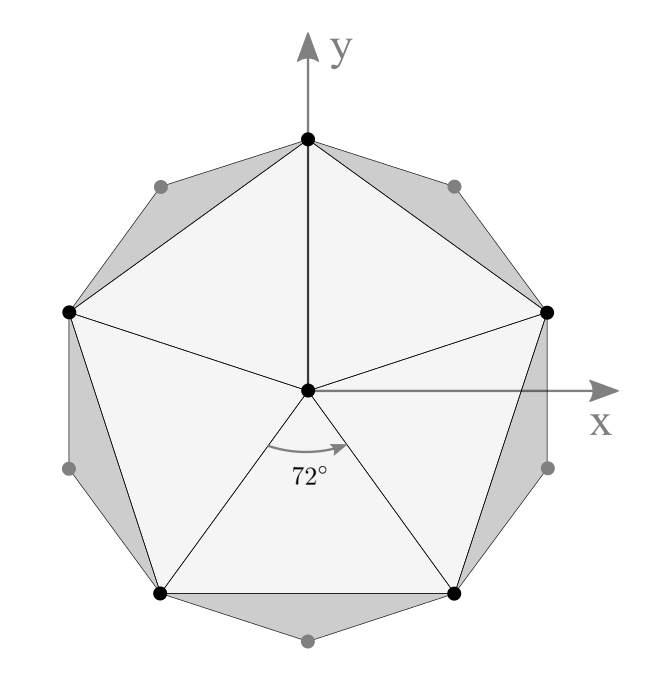 |
用球坐标可以简单地算出这些点来:
有了基础的正多面体,细分的过程就很容易了,分别区三角形三条边上的中点,并将中点投影到球壳上即可。可以用以下的伪代码来表述:
1 | Subdivide(triangles, radius) |
细分的效果大致如下所示,可以看到点的分布相比之前的UV球体要均匀了许多。
| 2次细分 | 4次细分 |
|---|---|
| 512个顶点,320个三角形 | 7820个顶点,5120个三角形 |
 |
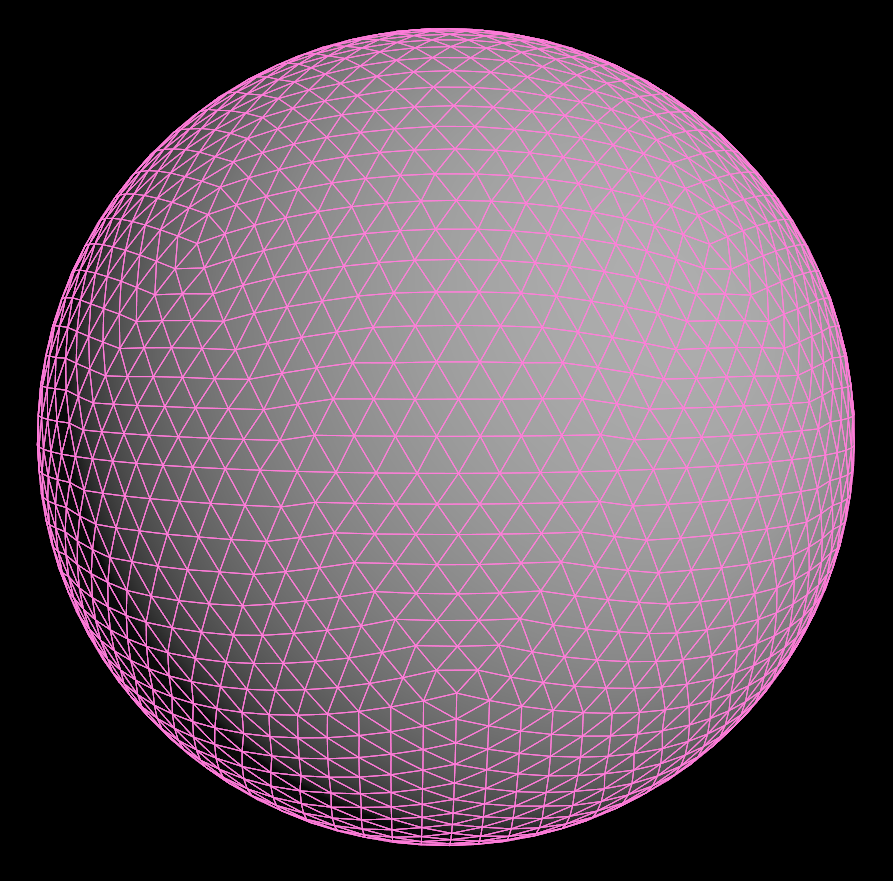 |
然而,这样细分出来的球体也不是十全十美的,它有一个致命的问题——就是贴图UV。由于细分的球体本身并不能直接得到贴图坐标,我们需要借助之前球坐标系的方法,应用其逆过程,将顶点坐标转换为球坐标再以两个角度作为UV。公式如下:
然而,当我们将贴图应用在球体上后,却会发现如下的效果:
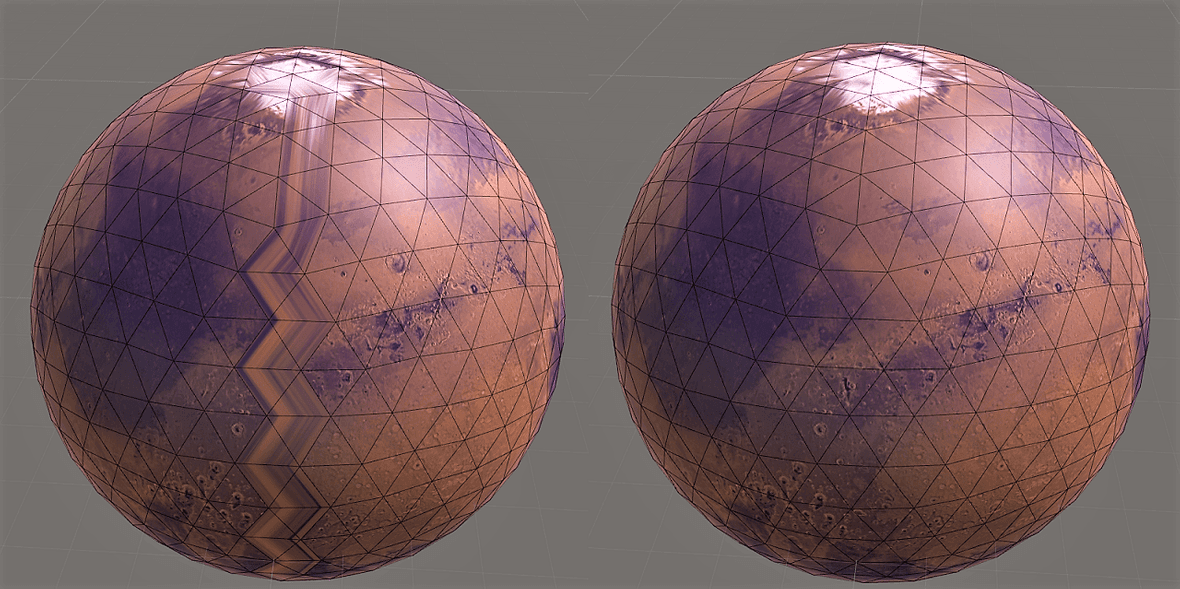
可以看到有一条明显Z型扭曲带,带上的三角形纹理好像被压缩了一样。很容易发现问题的原因:当贴图UV的值超过1.0时,由于转过了一圈,根据上面的式子算出的UV会回到0。这样就导致了在靠近这个UV边界的三角形内,UV的值一下子从接近1的地方跳跃到了接近0的地方,导致了贴图被压缩的现象。
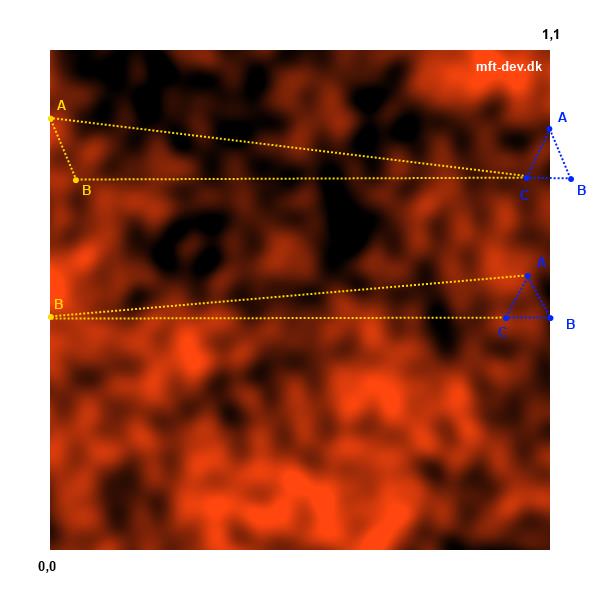
正如上图所示,本该是蓝色的三角形被映射到了黄色的三角形,导致了贴图的严重拉伸。要修复这个问题,只需把错误的三角形纠正过来就行。注意到这些错误的三角形,其顶点环绕顺序与正确三角形是相反的。原本的蓝色三角形是瞬时针环绕,被错误映射后变为了逆时针环绕。通过这个特征我们就可以发现错误的三角形了:只需要判断一下三角形的环绕顺序,即三角形两边的叉积的z坐标符号即可(虽然UV只是二维的点,但我们可以将其看做是z坐标为0的三维点,这样就可以进行叉乘运算了)。要为每个修正坐标的顶点生成一个新的顶点以解决共享顶点的问题。
这样处理完后,之前的Z字接缝就没有了。不过,在靠近两极的地方,UV仍有明显的扭曲。

问题显然还是因为共享顶点导致的UV坐标拉伸的缘故,从下图中可以明显看出来中间的三角形被严重拉伸。
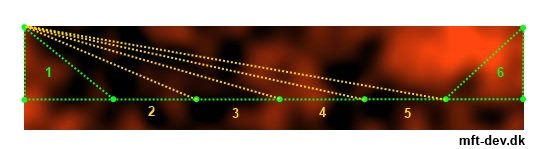
显然,两极的顶点对于每个三角形均需要不同的贴图坐标。然而问题是,该怎样得到UV呢?肯定不能用之前的式子算了,因为本身在处的值是没有良定义的。遗憾的是,这个问题没有一个完美的解决方案,因为在球顶的这块位置顶点重合,一整条边都对应到了一个点上,显然我们没法让其在贴图完美地对应到一个矩形区域里去。一种不太完美的解决方案是,将每个三角形贴图坐标的U取为下面两个顶点U的平均值。这样虽然球顶的顶点没有统一对应到一个UV上,但总的拉伸降到了最低。修改后的效果如下。
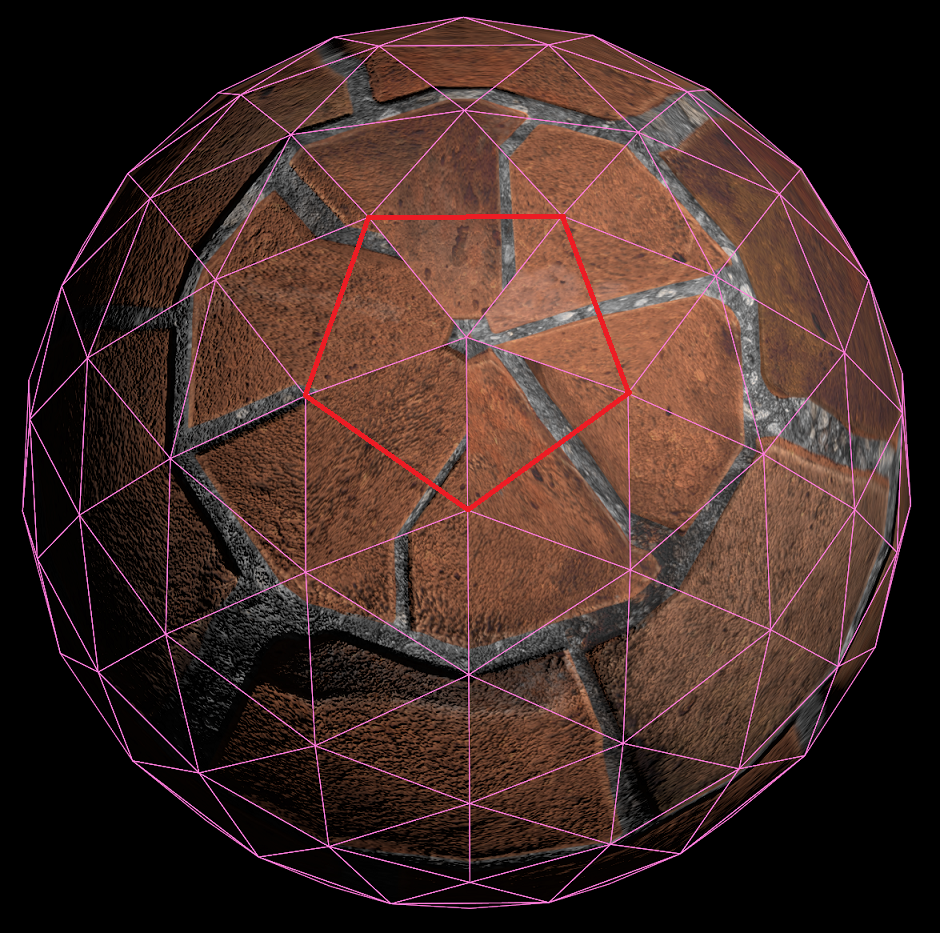
可以看到扭曲没有了,两个相连三角形的贴图有比较明显的接缝。这个接缝如果要解决的话,只能对贴图本身做处理了:将UV展开后让贴图上几何位置相邻的地方变化连续。事实上,将一个平面(贴图)包裹在一个球体上本身而没有扭曲的办法是不存在的,如果你对比过世界地图和实际的地球仪就会发现,靠近南北极的国家在地图上的大小要比实际的大小差很多。实际上,之前在UV球体上用的方法叫做Cylindrical Projection,其本质上是先把贴图卷成了一个圆柱体,然后再将其贴到球体上去,这就导致了约是靠近南北极的位置,贴图的扭曲就越大。
细分立方体(CubeSphere)
当然,细分还可以用其他的基础几何体来进行,这里再介绍一种使用立方体来进行细分的方式,这也是Unity中采用的球体。立方体的基础图元在这里是四边形,四边形的细分与三角形有细微不同但总体上类似:在四边形的四条边上取中点,还要在四边形的中间取一个点,再将中心的点与4个中点连起来,这样一个四边形就分割为4个小四边形。在有了细分后的立方体后,我们再按照上面讲过的方法,将点“投影”到球体上就可以了。当然,我们也可以直接一步到位地得到细分后的立方体,之后进行投影,效果是一样的。
| 无细分 | 1次细分 | 2次细分 | 3次细分 |
|---|---|---|---|
 |
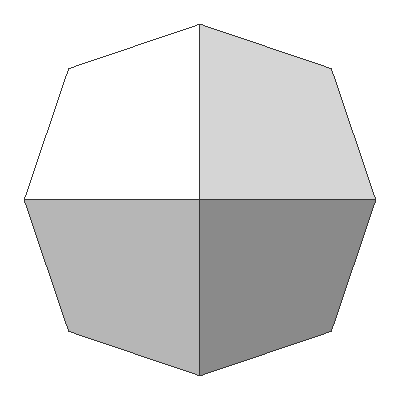 |
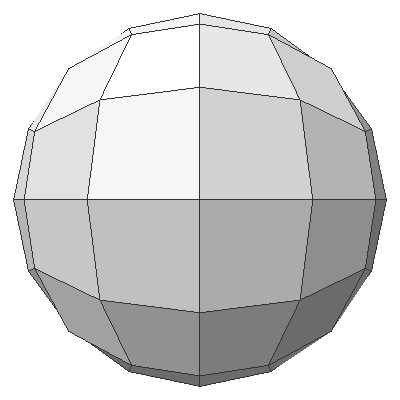 |
 |
如果按照之前的Cylindrical Projection的方式投影贴图,仍然需要像之前一样处理顶部与底部的错误UV。不过,细分立方球体还有更直接的贴图方式:由于其是由一个立方体变换来的,可以借用立方体的UV来进行处理。也就是说像Cubemap这样的贴图可以很方便地拿来使用。