高斯模糊是一种柔和模糊的图像效果。模糊后的图像可以被更复杂的算法用来产生形如炫光（bloom）、景深、热浪或者磨砂玻璃的效果。在本文中，我将会讲解如何利用高斯滤波器的种种优良特性来提高实现的效率，和利用贴图查找中双线性插值的特点，来大大提高高斯模糊效率的小技巧。虽然本文讲述的重点是高斯模糊滤波器，但其中大部分原理都可以运用在实时渲染中的其他卷积滤波器上。

**高斯模糊（Gaussian blur）**是图形学中一种常用的技术。不管我们讨论的是离线渲染器还是游戏引擎，许多渲染技术都需要它来产生可信的照片级效果。既然可编程图形管线早已出现，在片段着色器里采用高斯模糊或其他模糊滤波器俨然已经成为每一个游戏引擎必备的技术。

基础的卷积滤波算法极其消耗性能，然而许多显著降低计算量的优雅技巧，能使高斯模糊即便在老掉牙的硬件上也能流畅运行。这篇文章将会像教程一样，讲解大部分可行的优化技巧。其中一些技巧你可能已经听过，但线性采样（linear sampling）还是能给你一些惊喜。

让我们先从基础部分开始。

术语

为了提前消除你可能产生的疑惑，我会从介绍一些本文中出现术语和概念讲起。

卷积滤波器（Convolution filter）– 融合一组像素的颜色值的算法

NxN-tap滤波器（NxN-tap filter）– 使用NxN个像素的过滤器

N-tap滤波器（N-tap filter）– 使用1xN个像素的过滤器。注意一个N-tap滤波器并不意味着它必须要采样N个纹素，它也可以被实现为采样少于N个纹素。

滤波器核（Filter kernel）– 一组用来采样的相对坐标、权重集合

离散采样（Discrete sampling）– 恰好只读取一个纹素的采样方法（也就是 GL_NEAREST 采样）

线性采样（Linear sampling）– 读取2x2个纹素并双线性插值的采样方法（也就是 GL_LINEAR 采样）

高斯滤波器

图像空间的高斯滤波器是一个 NxN的卷积滤波器，它的采样权重基于高斯函数：

$G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}$

滤波器覆盖的像素将乘以一个有高斯函数得来的权重，来达成模糊的效果。高斯滤波器的空间表示（通常被称为“钟型曲线”），展示了每一个覆盖到的像素如果对最终的像素造成影响。

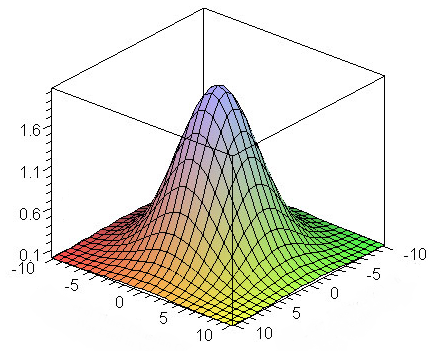
看到这个你也许会说：“啊哈，所以我们只需要做NxN次贴图读取然后把它们加权求和就OK了”。虽然是这样，它却没看起来那么高效。比如我们有一张大小为1024x1024的图片，然后用片段着色器实现基于这种方法的33x33高斯模糊滤波器，需要多达1024 * 1024 * 33 * 33 ≈ 11.4 亿次贴图读取才能在整张图片上应用这个模糊滤镜。

为了得到一个更高效的算法，我们需要分析一下高斯函数的一些良好性质：

• 二维高斯函数可以拆分为两个一维高斯函数计算

  $G(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}}$

• 一个有着$\sqrt2\sigma$分布的高斯函数$G_{\sqrt2\sigma}(x)$等价于两个有着$\sigma$的高斯函数$G_{\sigma}(x)$应用两次（注：原文此处表述有误，该性质的证明见此处）

这两个性质给了我们很大的优化空间。

基于第一个性质，我们可以将二维高斯函数分离为两个一维高斯函数。这意味着片段着色器的实现中，可以把高斯滤波器分为水平方向和垂直方向的滤波器，比如先应用水平方向的滤波器再应用垂直方向的滤波器，仍然可以得到与直接应用二维滤波器相同的结果。所以，我们最后只需要两个1xN滤波器和一次额外的渲染pass。回到我们的例子，在1024x1024大小的图片上应用两次1x33滤波器，我们需要1024 * 1024 * 33 * 2 ≈ 6900万次贴图读取。这个读取量就远远小于之前的方法了。

第二个性质可以用来绕过在一个pass中只能读取有限次贴图的硬件限制。

高斯卷积核的权重

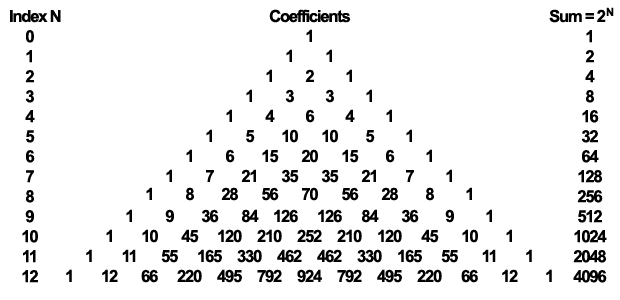
至少在理论上，我们已经看到了怎么高效地实现一个高斯模糊滤波器，但我们还没讨论为了得到最终的结果，滤波器怎么计算每一个像素所占的权重。最显而易见的方式是为不同坐标分布计算高斯函数的值来确定卷积核权重。虽然这是很通用的方法，但我们有一种更方便的计算权重的方法——二项式系数。为什么我们能怎么做？因为高斯函数其实是正态分布函数，而正态分布的离散形式就是采用二项式系数做加权的二项式分布。

帕斯卡三角形（杨辉三角）展示了二项式系数，它可以用来计算卷积核权重（每个元素是上一排的两个相邻元素的和）

为了实现我们的9x1水平滤波器和1x9垂直滤波器，我们将用上图帕斯卡三角形的最后一行来计算权重。你可能会问，为什么不用index为8的行（它刚好有9个数字）？这是个可证明的问题，但回答起来却很简单。这是因为在典型的32位颜色缓冲上最边上的系数对最终结果没有任何的影响。我们希望，在提供最佳质量的同时，使贴图读取次数最小化。显然，当我们需要高精度的结果，且有更高精度的颜色缓冲供我们使用时，用index为8的带小数的那行更好一些。但先回到我们原本的想法，使用最后一行…

有了必要的系数后，计算线性插值需要的权重就很简单了。我们只需将每个系数除以系数的总和（在这里是4096），当然，为了纠正消去最外层四个系数的影响，我们应该将总格减到4070，否则图片在运用几次滤波器后就会变暗许多。

现在，有了需要的权重，如何实现我们的片段着色器就显而易见了。我们来看看垂直滤波着色器的GLSL代码：

uniform sampler2D image;

out vec4 FragmentColor;

uniform float offset[5] = float[]( 0.0, 1.0, 2.0, 3.0, 4.0 );
uniform float weight[5] = float[]( 0.2270270270, 0.1945945946, 0.1216216216,
                                   0.0540540541, 0.0162162162 );

void main(void)
{
    FragmentColor = texture2D( image, vec2(gl_FragCoord)/1024.0 ) * weight[0];
    for (int i=1; i<5; i++) {
        FragmentColor +=
            texture2D( image, ( vec2(gl_FragCoord)+vec2(0.0, offset[i]) )/1024.0 )
                * weight[i];
        FragmentColor +=
            texture2D( image, ( vec2(gl_FragCoord)-vec2(0.0, offset[i]) )/1024.0 )
                * weight[i];
    }
}

显然水平滤波器只是将偏移值从应用在Y坐标上改变为应用在X坐标上。注意，在除以1024以得到屏幕空间的坐标时，我们硬编码了图片的大小。在实际应用中，我们可能会用一个uniform替代它，或直接使用不需要归一化纹理坐标的纹理矩形。

如果你不得不多次应用滤波器来得到更强烈的效果，唯一要注意的事情是在两个帧缓冲间切换，将着色器应用在前一步保存结果的帧缓冲上。

1x9和9x1的滤波器应用在大小为1024x1024的图片上：原始图片（左边）、应用1次（中间）、应用9次（右边）。

线性采样

到此为止，我们已经知道怎么实现一个分离两次渲染的高斯滤波器。我们也看到了，在1024x1024 的图片上可以使用这个滤波器九次来得到33x33大小的滤波器的效果，仅仅只需5千6百万次贴图读取。尽管这已经很高效了，它并没能完全利用到GPU的优势，因为这种算法也能毫无修改，完美地运行在CPU上。

现在，我们已经可以利用GPU提供的固定功能硬件管线来进一步减少贴图读取的次数。为了达到优化的目的，让我们先回顾一下这篇文章开头所作的一个假设。

到此为止，我们假设了我们必须要做一次贴图读取来获得一个像素的信息，意味着9个像素需要9次贴图读取。尽管这对于在CPU上的实现来说是成立的，但在GPU上却不总是这样。这是因为在GPU上我们能随意地使用双线性插值（bilinear sampling）而没有什么额外的负担。这意味着如果我们不在纹素中心读取贴图，我们就可以得到多个像素的信息。既然我们已经利用了高斯函数的可分离性，实际上是在1D下工作，双线性插值会给我们提供2个像素的信息。每个纹素贡献对颜色的贡献量则由我们使用的坐标决定。

通过正确地调整贴图读取的坐标偏移我们可以仅通过一次贴图读取得到两个像素或纹素的准确信息。这意味着为了实现一个9x1或1x9的高斯滤波器我们只需要5次贴图读取。总的来说，Nx1或1xN的滤波器我们需要[N/2]次贴图读取。

这对我们之前为离散样本高斯滤波器使用的权重值有什么意义呢？这意味着每种情况下我们使用单次的贴图读取获得了两个纹素的信息，我们需要用其乘以两个纹素对应的权重和所计算出的新权重。既然我们知道了权重是什么，我们现在只需要计算正确的纹理坐标偏移了。

我们可以简单地用两个纹素中心点的中间坐标作为纹理坐标。虽然这是一个好的近似，我们并不会使用它——因为我们能计算出更好的坐标，得到与离散采样一模一样的效果。

对于两个纹素的合并，我们需要调整坐标使其与纹素#1中心的距离等于纹素#2的权重除以两个权重之和。同样的，坐标与纹素#2中心的距离应该等于纹素#1的权重除以两个权重之和。

然后我们就有了计算线性采样高斯滤波的权重和位移公式：

$weight_L(t_1,t_2)=weight_D(t_1)+weight_D(t_2)\\ offset_L(t_1,t_2)=\frac{offset_D(t_1) \cdot weight_D(t_1) + offset_D(t_2) \cdot weight_D(t_2)}{weight_L(t_1,t_2)}$

为了使用这个信息，我们只需替换uniform常量并减少纵向滤波器shader中迭代的次数，得到：

uniform sampler2D image;

out vec4 FragmentColor;

uniform float offset[3] = float[]( 0.0, 1.3846153846, 3.2307692308 );
uniform float weight[3] = float[]( 0.2270270270, 0.3162162162, 0.0702702703 );

void main(void)
{
    FragmentColor = texture2D( image, vec2(gl_FragCoord)/1024.0 ) * weight[0];
    for (int i=1; i<3; i++) {
        FragmentColor +=
            texture2D( image, ( vec2(gl_FragCoord)+vec2(0.0, offset[i]) )/1024.0 )
                * weight[i];
        FragmentColor +=
            texture2D( image, ( vec2(gl_FragCoord)-vec2(0.0, offset[i]) )/1024.0 )
                * weight[i];
    }
}

这个简化后的算法是数学正确的，如果不考虑硬件实现的算线性插值可能带来的舍入误差，我们的线性采样shader将得到和离散采样一样的结果。

使用9次9x1高斯模糊，分别采用离散采样（左）和线性采样（右）。注意到我们的两种实现甚至在多次pass后仍然没有视觉上的区别。

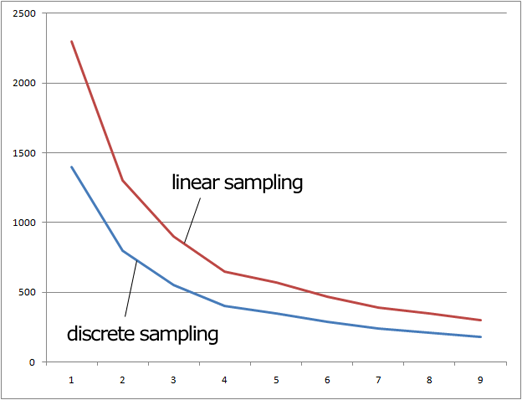
尽管线性采样的实现非常简单，它仍在高斯模糊滤波器上有显著的视觉效果。考虑到我们设法只用了5次的贴图读取而非9次就实现了一个9x1的滤波器，再回到我们的例子，用33x1大小滤波器模糊一张1024x1024的图片只需 1024 * 1024 * 5 * 3 * 2 ≈ 3100万次纹理读取，而不是离散采样需要的5600万次读取。这是一个合理的区别，为例体现有多大的提升，我做了一些实验来测量两种实现的区别。结果如下：

使用9x1高斯模糊，分别采用离散采样和线性采样的性能区别。（在Radeon HD5770上测试）纵轴是每秒帧率（越高越好），横轴是模糊的次数（越高越模糊）。

我们可以看到，线性采样实现的高斯模糊的性能比离散采样实现的高了60%，不管对图片模糊了多少次。这与线性采样省下的贴图读取次数大致呈正比。

结论

我们已经了解到实现一个高效的高斯模糊滤波器是十分简单的，尤其是使用线性采样的时候，得到了一个速度极快的实时算法，而它可以作为更高级的渲染技术的基础。

尽管这篇文章只讨论了高斯模糊，让其中的原理可以应用在绝大多数卷积核类型。除此之外，大多数理论要求我们模糊一张大小缩减的图片，比如光晕效果（bloom）就经常有这个要求。对于大小缩减的图片的情况来说，唯一的区别就是我们的中心像素也是一个“双重像素”。这意味着我们必须用帕斯卡三角形中有着偶数个系数的行，因为我们也想要线性采样中间的纹素。

我们也简要地介绍了不同实现的计算复杂度，并说明了怎么在GPU上高效地实现滤波器。

演示不同采样性能差别的示例程序可以在这里下载：

Binary release

Platform: Windows
Dependency: OpenGL 3.3 capable graphics driver
Download link: gaussian_win32.zip (2.96MB)

Source code

Language: C++
Platform: cross-platform
Dependency: GLEW, SFML, GLM
Download link: gaussian_src.zip (5.37KB)

---

原作者：Daniel Rákos

创作时间： September 7, 2010

发布地址： http://rastergrid.com/blog/2010/09/efficient-gaussian-blur-with-linear-sampling/